That happens when they are linearly independent. We prove that the set of three linearly independent vectors in R3 is a basis.

Does A Set Of Vectors Span R N Youtube
Same with R3 when they span R3 then they take up all the space in R3 by some combination of them.

. If r3 and the vectors are in R3 then this must be the whole space. For an arbitrary v 2R3. Fin300 fin 300 fin401 fin 401 qms 102 qms 101 qms10 adms 3530 adms3530 adms 4501 adms 4502 ryerson university york univer.
If there is always a solution then the vectors span mathbbR3. Consider the linear combination x1 1 0 1 x2 2 1 1 x3 2 1 4 0. Show that H is a subspace of R3.
Our aim is to solve the linear system Ax v where A 2 4 1 2 4 1 1 3 4 3 5 3 5and x 2 4 c 1 c 2 c 3 3 5. If you liked my science video yo. When vectors span R2 it means that some combination of the vectors can take up all of the space in R2.
You must log in or register to reply here. They are linearly independant which means they span a subspace of dimension 3 but since the space is R 3 span u v w R 3. Three such vectors span R3 iff they are linearly independent.
Linear dependant vectors cannot span. How to determine if vectors span r3. We must be talking about vectors of the form abc.
Support Author Jonathan David. Please support my work on Patreon. Also a spanning set consisting of three vectors of R3 is a basis.
If there is a choice of abc for which the system is inconsistent then the vectors do not span mathbbR3. This has a solution only when 7x11y z 0. To your second question if you have three vectors and rref the set spans R3 if you have three pivots.
Forums Free Math Help. R4 is 4 dimensions but I dont know how to describe that. If your last row is only zeros then the set does not span R3.
You can use the same set of elementary row operations I used in 1 with the augmented matrix leaving the last column indicated as expressions of a b and c. Span 1 3 2 6 is 1-dimensional as 1 3 12 x 2 6 Span 1 0 0 0 1 0 1 1 0 is 2-dimensional as 1 0 0 0 1 0 1 1 0 To predict the dimensionality of the span of some vectors compute the rank of the set of vectors. However thats not the only way to do it.
Try to find if they are linearly independent which can be done by as mentioned before trying to row reduce the 3x3 matrix you get by putting the 3 together. 3 vectors in R3 span R3 if they are linearly independent. R3 is the xyz plane 3 dimensions.
Three Vectors Spanning R3 Form a Basis. You need three vectors to span R3 you have two so the answer is no. Let x1x2x s be vectors in Rn.
In a matrix the vectors form. Happy is so three you gives us three a six B and nine C minus 12 of the negative to a 12 of B and negative C so this gives us three minus. Now if you have n such vectors if any three are independent then they all span R3.
See the post Three Linearly Independent Vectors in R3 Form a Basis. This comes from the fact that columns remain linearly dependent or independent after any row operations. Then using row operations convert M into RREF.
The columns - or rows - of a rank r matrix will span an r-dimensional space. For the proof of this fact a S 1 0 1 2 1 1 2 1 4 Let us check that whether S is a linearly independent set. For example you could look at the null space and use the rank-nullity theorem.
If v xyz reduce the augmented matrix to 2 4 1 2 4 x 0 1 1 x y 0 0 0 7x11y z 3 5. As s columns are not linearly independent neither are the vectors in your questions. Since we have that given n vectors v 1 v n K n these are linearly independant if and only if det v 1 v n 0.
Its a years since I took Linear Algebra so I give no guaranties. Thus the span of these three vectors is a plane. If you get the identity they are linearly independent if you get a zero row they are linearly dependent and therefore do not.
A set of 3 vectors in R3 is linearly independent if the matrix with these vectors as columns has a non-zero determinant.

Linear Algebra Why A Inconsistent System Can Be Considered As A Span Updated Example Added Mathematics Stack Exchange
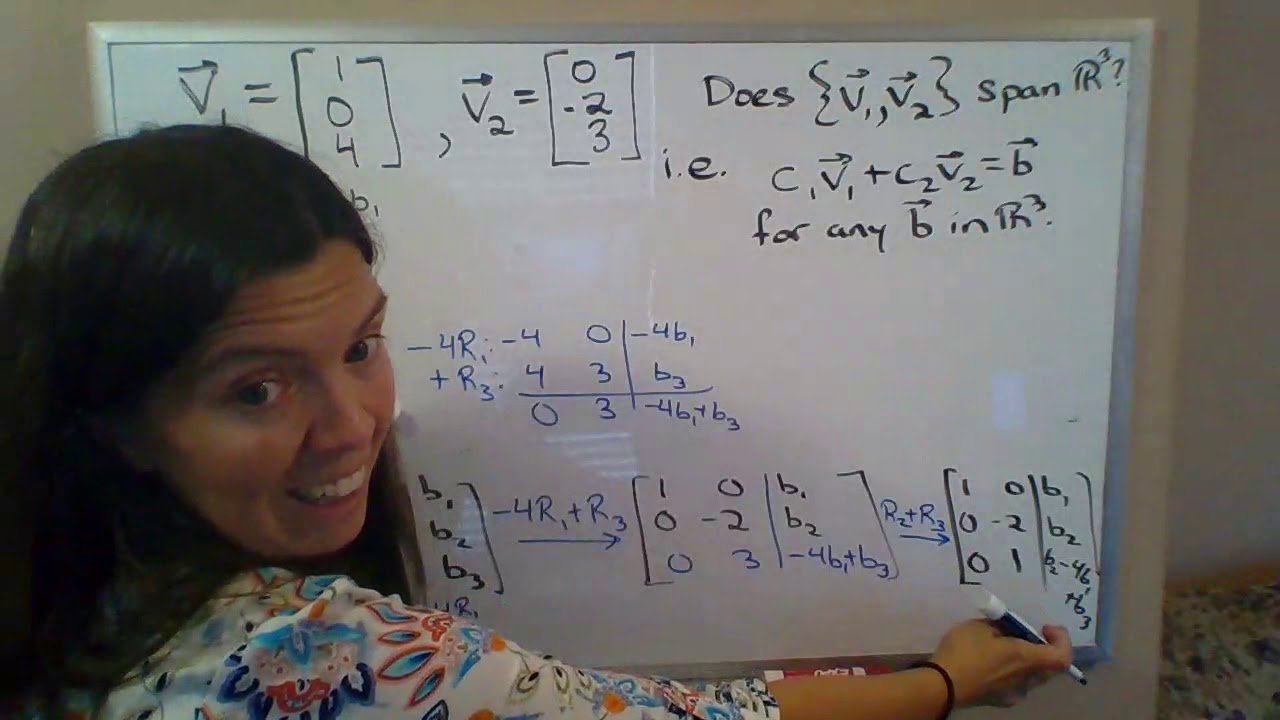
Determine Whether A Collection Of Vectors In R 3 Spans R 3 Youtube

Solved 3 Show That Span R3 Are All Vectors Necessary To Chegg Com

0 Comments